Perspective Projection
Dealing With Overlaps
If you look closely at the code from the previous article you’ll notice that all the statements are carefully ordered in the code. This is because when it comes down to actually drawing lines, if line A is drawn before line B, it will get obscured by it.
When projecting to 2d, this might give the impression that line A is behind line B while this might not actually be the case.
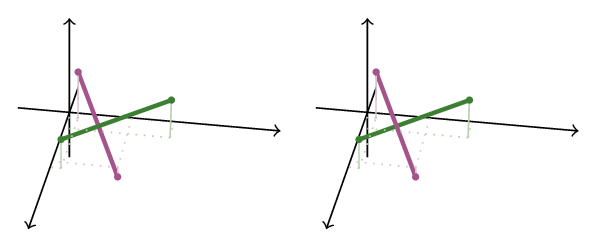
Which of the above is the truer representation?
We are interested in devising a method for ordering segments so that they get rendered far-to-near (a.k.a the painter’s algorithm).
We’ll start with two segments in 3d space:
\[\mathbf{AB} = \left\lbrace \vec A + t (\vec B - \vec A) | t \in \left[0..1\right] \right\rbrace \\ \mathbf{CD} = \left\lbrace \vec C + s (\vec D - \vec C) | s \in \left[0..1\right] \right\rbrace\]In addition, as you might imagine, occlusion depends on where you stand and where you look, so our observer will be standing at at $\vec V$ looking in the direction $\hat D$ at a screen at distance $l$. This observer observes that the segments intersect. To figure which of them should overlap the other, we need to follow these steps:
- Project both segments on the plane
- Find the intersection point
- Cast a ray from the viewer to the intersection point, and find the ray’s intersection with both segments
- Determine which intersection point is farther from the viewer - that segment should be drawn first
Project
We are dealing with two segments: $\mathbf{AB}$ and $\mathbf{CD}$.
First we cast each vertex onto the viewer’s plane (we will use lowercase vectors for vectors on the screen):
\[\vec a = \vec V + \frac{l}{\hat D \cdot \left(\vec V - \vec A\right)} \left(\vec V - \vec A\right)\]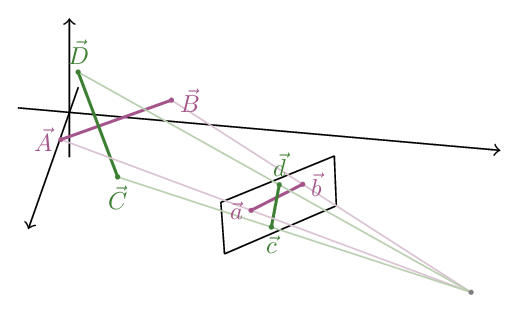
Intersect
We now have two peojected segments on the surface of the viewer’s plane: $\mathbf{ab}$ and $\mathbf{cd}$
Checking for an intersection
Each segment lies on a line which can be written as:
\[\vec r(t) = \vec a + t \left(\vec b - \vec a\right)\]If we cross ($\times$) both sides of the equation with $\vec b - \vec a$ we can obtain a non-parametric equation for $\vec r$ (a.k.a. locus):
\[\vec r \times \left(\vec b - \vec a\right) = \vec a \times \left(\vec b - \vec a\right) \\ \Rightarrow \left(\vec r - \vec a\right) \times \left(\vec b - \vec a\right) = \vec 0\]This is just a way to say that $\vec r - \vec a$ is aligned with $\vec b - \vec a$.
But, what if we replace $\vec r$ with a vector’s that’s not on the line. What does the expression evaluate to?
If $\vec r$ is outside the line, then according to the right hand rule the cross product $\left(\vec r - \vec a\right) \times \left(\vec b - \vec a\right)$ will be perperdicular to both terms.
But we also know that $\vec r$ is on the plane, and so both terms are embedded in the plane as well, which means that their cross product must be in the direction of the normal to the plane $\hat n$.
However, “in the direction” can also mean in the opposite direction. What decides whether the product is in the direction of $\hat n$ or $-\hat n$?
According to the right hand rule, the rule holds only if the angle between the two vectors is smaller than $180^\circ$. If it’s more that that, we need to flip the order of the vectors so that we form the smaller angle between them, and as a consequence, the direction of the product flips ($\mathbf{ab}$ is black, $\vec{r}$ is blue and the cross product $\left(\vec r - \vec a\right) \times \left(\vec b - \vec a\right)$ is red):
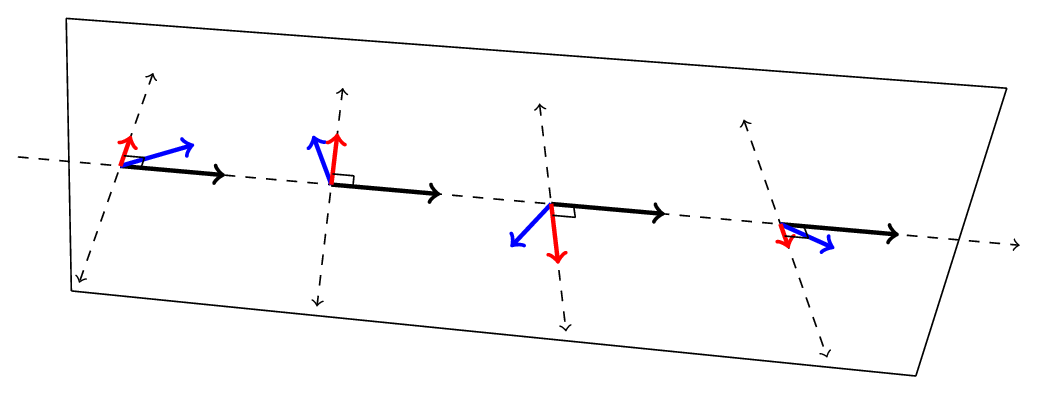
This is very important, because that $180^\circ$ angle forms a border: vectors that point to one side will result in a product that’s in the direction of $\hat n$, and points on the other side will result in a product in the direction of $-\hat n$, while all the points that lie on the border will result in a product that’s perpendicular to $\hat n$.
We can summarize this:
\[\left[\left(\vec r - \vec a\right) \times \left(\vec b - \vec a\right)\right] \cdot \hat n \begin{cases} < 0 & \textrm{right of } \mathbf{ab} \\ = 0 & \textrm{on } \mathbf{ab} \\ > 0 & \textrm{left of } \mathbf{ab} \end{cases}\]Of course right and left are arbitrary, but you get the idea.
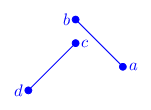
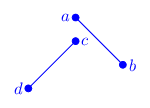
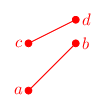
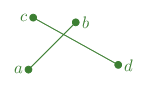
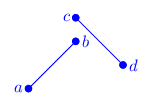
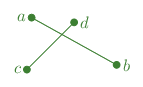
There is a total of 16 configuration of both segments in relation to where each vertex lies in relation to the other segment (each vertex can be either to the left or right of the other segment, and there is a total of 4 vertices, so: $2^4=16$). Granted, many of these configuration are equivalent, but just for the sake being thorough, we’ll list all of them:
| ab=ll | ab=lr | ab=rl | ab=rr | |
|---|---|---|---|---|
| cd=ll |  |
 |
 |
 |
| cd=lr | 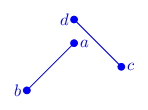 |
 |
 |
|
| cd=rl | 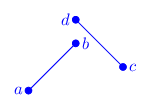 |
 |
 |
|
| cd=rr |  |
 |
 |
 |
As you can see, due to $a \leftrightarrow b$, $c \leftrightarrow d$ and $\mathbf{ab} \leftrightarrow \mathbf{cd}$ symmetries, there are three configurations (grouped by color), only one of which is that of intersecting segments. The blank cells are impossible configurations (I’ll leave this as a thought exercise to you).
As you can see, intersections only occurr if
- $\vec{a}$ and $\vec{b}$ are on opposite sides of $\mathbf{cd}$ and
- $\vec{c}$ and $\vec{d}$ are on opposite sides of $\mathbf{ab}$
What’s the mathematic interpretation of both conditions? Well, if we take the first condition, this means that either:
- $\left[\left(\vec a - \vec c\right) \times \left(\vec d - \vec c\right)\right] \cdot \hat n > 0$ and $\left[\left(\vec b - \vec c\right) \times \left(\vec d - \vec c\right)\right] \cdot \hat n < 0$
- $\left[\left(\vec a - \vec c\right) \times \left(\vec d - \vec c\right)\right] \cdot \hat n < 0$ and $\left[\left(\vec b - \vec c\right) \times \left(\vec d - \vec c\right)\right] \cdot \hat n > 0$
In other words, the signs of $\left[\left(\vec a - \vec c\right) \times \left(\vec d - \vec c\right)\right] \cdot \hat n$ and $\left[\left(\vec b - \vec c\right) \times \left(\vec d - \vec c\right)\right] \cdot \hat n$ are opposite. Which means their product must be negative!
Which means that the conditions for intersection are:
\[\left\{\left[\left(\vec c - \vec a\right) \times \left(\vec b - \vec a\right)\right] \cdot \hat n\right\} \left\{\left[\left(\vec d - \vec a\right) \times \left(\vec b - \vec a\right)\right] \cdot \hat n\right\} < 0 \\ \textrm{and}\\ \left\{\left[\left(\vec a - \vec c\right) \times \left(\vec d - \vec c\right)\right] \cdot \hat n\right\} \left\{\left[\left(\vec b - \vec c\right) \times \left(\vec d - \vec c\right)\right] \cdot \hat n\right\} < 0\]Finding the intersection
Ok, now suppose the condition passes and we know there’s an intersection, how do we find it?
This is actually a geometric problem: we have a quadrilateral whose diagonals are the segments, and we want to find the ratio with which the segments divide each other.
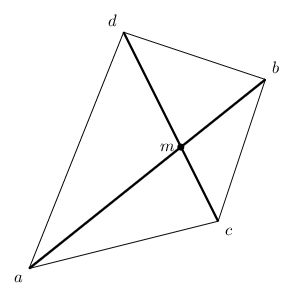
From the law of sines we obtain:
\[\frac{\mathbf{am}}{\sin(\angle mca)} = \frac{\mathbf{cm}}{\sin(\angle mac)} \\ \frac{\mathbf{bm}}{\sin(\angle mcb)} = \frac{\mathbf{cm}}{\sin(\angle mbc)}\]If we divide both equations, and rearrange them, we can obtain the division ratio of the $\mathbf{ab}$ diagonal:
\[\frac{\mathbf{am}}{\mathbf{bm}} = \frac{\sin(\angle mca) \sin(\angle mbc)}{\sin(\angle mcb) \sin(\angle mac)}\]Where do we get the sine of these angles? Well, first we observe that $\angle mca = \angle dca$. And then we use the geometric meaning of the cross product to obtain:
\[\sin(\angle mca) = \sin(\angle dca) = \frac{\left|\vec{cd}\times\vec{ca}\right|}{\left|\vec{cd}\right| \left|\vec{ca}\right|}\]Following the same for the rest of the angles we get:
\[\frac{\mathbf{am}}{\mathbf{bm}} = \frac{\left|\vec{cd}\times\vec{ca}\right| \left|\vec{ba}\times\vec{bc}\right|}{\left|\vec{cd}\times\vec{cb}\right| \left|\vec{ab}\times\vec{ac}\right|}\]And finally, the intersection point:
\[\vec{m} = \frac{1}{1 + \frac{\mathbf{am}}{\mathbf{bm}}}\vec{a} + \left(1 - \frac{1}{1 + \frac{\mathbf{am}}{\mathbf{bm}}}\right)\vec{b}\]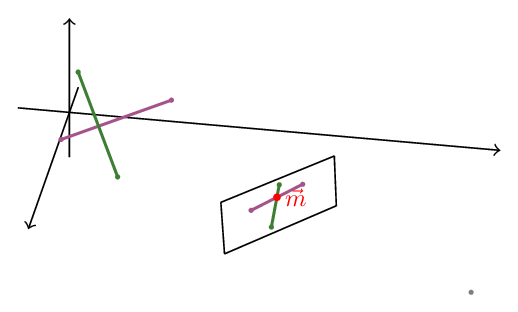
Project back
We will now cast a ray from the viewer ($\vec V$) through $\vec m$:
\[\vec M = \vec V + \alpha \left(\vec m - \vec V\right)\]This should intersect with the each of the segments at points which correspond to $\vec m$ on the screen.
\[\vec M(\alpha) = \vec A + t \left(\vec B - \vec A\right) \\ \vec V + \alpha \left(\vec m - \vec V\right) = \vec A + t \left(\vec B - \vec A\right) \\ \alpha \left(\vec m - \vec V\right) \times \left(\vec B - \vec A\right) = \left(\vec A - \vec V\right) \times \left(\vec B - \vec A\right) \\ \alpha = \frac{\left|\left(\vec A - \vec V\right) \times \left(\vec B - \vec A\right)\right|}{\left|\left(\vec m - \vec V\right) \times \left(\vec B - \vec A\right)\right|}\]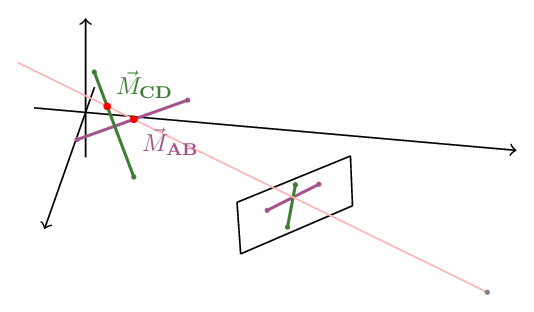
We now just need to compare $\alpha$ and $\beta$ to determine which segment occludes which:
V = observer._camera_position
for i in range(len(segments)):
ab = segments[i].project_to(observer)
for j in range(i + 1, len(segments)):
cd = segments[j].project_to(observer)
if not does_intersect(ab.vertices, cd.vertices, observer.screen):
continue
m = intersect(ab.vertices, cd.vertices)
alpha = distance_to_segment(V, m, segments[i].vertices)
beta = distance_to_segment(V, m, segments[j].vertices)
if alpha < beta:
segments[i], segments[j] = segments[j], segments[i]
Complicated occlusion
Actually, we’re not done yet. Support we have the following situation:
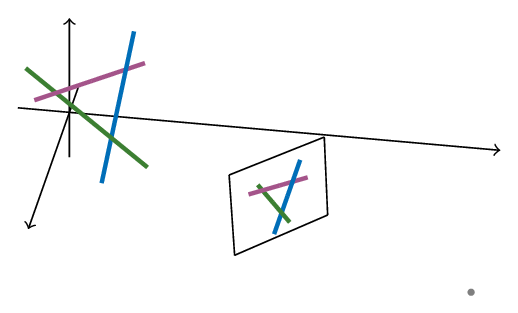
There we have:
- Green occluding blue and occluded by purple
- Blue occluding purple and occluded by green
- Purple occluding green and occluded by blue
There isn’t really a way to order the three segments because for each of them it’s both in front and behind the other two.
To overcome this we are going to have to break them into segments that have only one intersection with any other segment.
The strategy is pretty simple:
- Cast all the segments to the screen.
- For each segment, find all possible intersections with all the other segments.
- Trace back the point to a point on the 3d segment
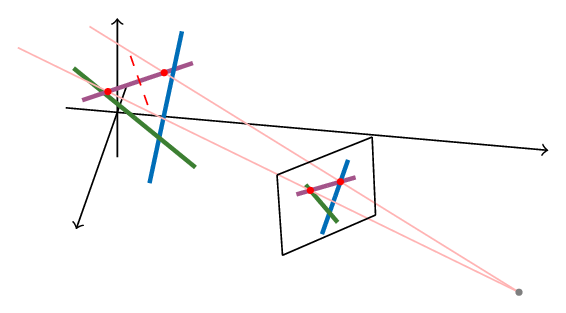
- Break the segment into smaller pieces between intersections (requires sorting the intersections points)
V = observer._camera_position
fragments = []
for segment in self._segments:
intersections = []
for other in self._segments:
if segment == other:
continue
ab = segment.project_to(observer)
cd = other.project_to(observer)
if not does_intersect(ab.vertices, cd.vertices, observer.screen):
continue
m = intersect(ab.vertices, cd.vertices)
M = intersect_ray_with_segment(V, m, segment.vertices)
intersections.append(M)
if len(intersections) > 1:
start = segment.vertices[0]
intersections.sort(key=lambda i: (i - start) & (i - start))
midpoints = [(a + b) / 2 for a, b in pairwise(intersections)]
fragments.extend(segment.fragment(midpoints))
else:
fragments.append(segment)
segments = sort_segment(fragments)
Here’s an example that combines all the elements in this article:
I went ahead and pushed the new code to the 3dpp repository together with some other improvements and documentation. Be sure to check it out!